Ich bin kein Coder, aber ich wäre gern ein Programmierer. Manchmal habe ich so tolle Ideen, kann die aber mangels passendem Wissen und Fähigkeiten nicht umsetzen. Und mein Lieblings-PHP-Coder funktioniert leider nicht auf Zuruf (außerdem schafft der kaum seine eigenen Projekte (aber das ist ja unser aller Problem)).
Schon vor über vierzig Jahren saß ich vorm ZX-81 und gab über die vielen Tastenkürzel irgendwelchen Code ein, der zwar meist lief, den ich aber nie speichern konnte, weil das mit den doofen Kassetten nie ging. Am Amiga wollte ich dann C# lernen. Das Buch dazu habe ich neulich in einem verstaubten Regal gefunden. Das C64-Basic beherrschte ich einigermassen und konnte mir damit immerhin die grundlegenste Programmierlogik verinnerlichen. Warum ich euch das alles erzähle? Ihr werdet staunen:
Auf all meinen letzten iPhones habe ich immer eine Solitair-App mit „durchgeschlurrt“. Bei jedem neuen Gerät kam die per Backup wieder drauf. Und ich achtete peinlich darauf, nie ein Update für diese App zu laden. Das ist so eine Kartenspiel-App mit ganz vielen Varianten. Vor vielen Jahren hatte ich mal die Idee: Bei jeder Variante will ich 100 Spiele gewinnen, dann kommt die nächste dran, bis alle durch sind, dann kann die App wieder weg. Klar, das dauert vermutlich Jahre, doch sone App is ja toll, wenn man mal Zeit überbrücken muss und kein Bock auf Lesen hat: Im Bus, beim Warten auf den Zug, lang auf der Couch, beim ka… ihr wisst schon. Eine Variante foppte mich: Das war wohl eine von diesen, die nicht immer lösbar sind, also begann ich ein neues Spiel. Ein (1) Spiel verloren. Dann kam ich dahinter und stellte fest, dass doch jedes Spiel erfolgreich abgeschlossen werden kann, man muss nur ggf. sehr tüfteln. Dann hatte ich 99 Spiele gewonnen. 99%. Hm. Ich spielte weiter. Irgendwann hatte ich 99,x% und begann im Kopf zu überschlagen, wie viele Spiele ich noch gewinnen müsste, um x+1 zu
erreichen: Wenn die Gesamtzahl der Spiele 102 beträgt, dann wäre ein Prozent 1,02 Spiele. Also müsste ich die Anzahl der gewonnenen Spiele (101) durch die 1,02 Spiele teilen und hätte die Quote: Das kriege ich im Kopf nur so weit hin, dass ich wusste: Das ändert sich auschliesslich im Nachkommabereich. Und mein Genius stellte gleich fest: Für jede einzelne Steigerung der Quote musste ich jeweils immer mehr Spiele gewinnen, das war natürlich nicht linear. Damals nahm ich mir vor, von jeder hundertstel Prozent-Punkte-Steigerung einen Screenshot zu machen, denn ich wollte das gerne analog lösen, konnte es aber nicht errechnen. Dann wollte ich irgendwann, wenn ich genug „Punkte“ gesammelt habe, ein Koordinatenkreuz erstellen, wo sich eine steigende Kurve ergeben müsste. Je nach Feinheit und Genauigkeit müsste ich extrapolieren können, wann die nächste Stufe erreicht wird. Oh, das klang spannend!
Anfang Februar 2024 hatte ich 1543 Spiele und die Quote sprang um ein zehntel auf 99,94%. Mein Gedanke dabei: Wann würde er wohl auf 100% aufrunden? 99,95% wird vermutlich nicht reichen, da fehlen ja noch einige Zehntel. Aber ich hatte nun sechs „Punkte“ für meine zeichnerische Lösung: In QCAD zeichnete ich eine waagerechte Linie und teilte sie in 10 Teile. Das war die Prozent-Skala, beginnend bei 99,88. Die jeweils dazu passende Anzahl der Spiele trug ich als senkrechte Linien ein. Die Länge der Linien entsprach der Anzahl Spiele. Wenn ich nun die Endpunkte verbinde, hätte ich eine „Quasi“-Kurve, anhand der ich vielleicht Zwischen- oder folgende Punkte ermitteln konnte. Es machte richtig Spaß, dass zu „konstruieren“, doch das Ergebnis verwunderte mich. Hier ein Bild von der ermittelten Kurve. Die durchgehende obere Linie zwischen Low und High dient nur der besseren Visualisierung:
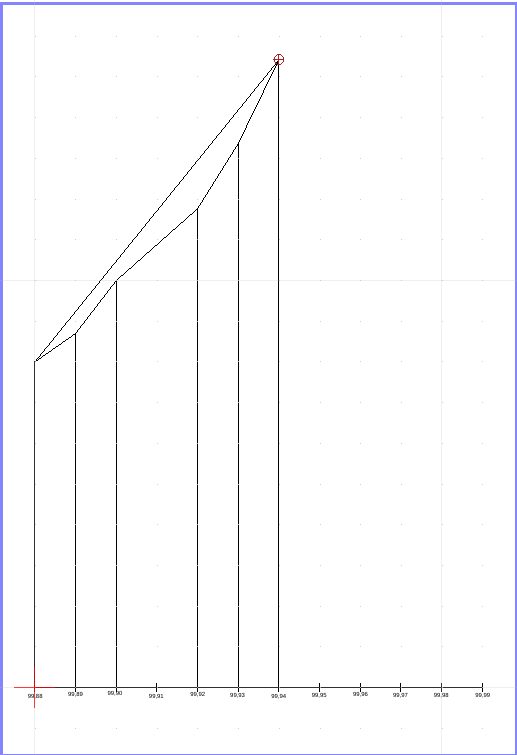
Nanu? Man erkennt klar am dritten Punkt von links: Da ist ein Ausschlag nach oben. Wie kann das sein? Ich will ja gerne vermuten, dass ich meine Daten, die Screenshots, nicht immer Spielgenau erfasst habe, aber da würde es sich um wenige Spiele handeln. Zumal der dritte das 999. Spiel ist, mit einer Quote von 99,90%. Das passt doch glatt! Sind alle anderen ungenau? Das mochte ich nicht glauben! Ich musste mich doch rechnerisch rantasten. Aber das würden solche Zahlenkolonnen, das geht nicht mehr sinnvoll analog. Nun entsann ich mich nicht nur meiner rudimentären Basic-Kenntnisse sondern mir fiel auch ein, dass ich vor einiger Zeit mal Basic-256 auf meinem Ubuntu-Lappi installierte (weil ich mir alle paar Jahre ganz fest vornehme, doch mal eben Programmieren zu lernen und das bald darauf wieder einschlafen lasse. Man kann nicht alles.)
Da ich noch weiss, was Schleifen und Variablen sind und wie man die verwendet und weil das Basic-256 wirklich schön einfach ist (nicht mal Zeilennummern wie beim Commodore Basic 2.0), brachte ich überraschend schnell folgenden Code zustande:
for Sp = 100 to 2000
pro = Sp/100
quo = (Sp-1)/pro
GW = Sp – 1
Print „bei “ + gw + “ gewonnenen Spielen betraegt die Quote:“ + quo
Next
Ich habe da eigentlich mindestens eine Variable zu viel drin, weil ich in der ersten Version eine Fehlermeldung erhielt und nicht erkannte, was ich falsch gemacht hatte (ach, da werden dann doch Zeilennummern verwendet):
COMPILE ERROR on line 5: Syntax error around character 16.
Das 16. Zeichen war irgendwo bei der Variable und ich kam nicht drauf. Setzte ich ein REM vor die Print-Zeile und ersetzte sie durch „print quo“, dann rasselte es (nachdem ich das von mir vergessene Next ergänzt hatte) voll durch. Aber es gab eben nur eine unformatierte Zahlenkolonne als Ausgabe. Ein Blick in die Hilfe half: Ich musste die einzelnen Werte für den Print-Befehl addieren, also jeweils ein „+“ dazwischen setzen. Kaum macht mans richtig, schon funktioniert es. Die Ergebnisse sicherte ich in einem 37 seitigen PDF. Nun konnte ich einzelne Werte kontrollieren!
Spiele – % im Spiel – % errechnet
799 – 99,88 – 99,875
869 – 99,89 – 99,885
999 – 99,90 – 99,90
1176 – 99,92 – 99,915
1336 – 99,93 – 99,9252
1542 – 99,94 – 99,93519
Eigentlich sauber aufgerundet, oder? Bei den letzten beiden Werten war es interessant, denn 99,925% waren rechnerisch schon bei 1333 erreicht. Für 99,94% hätten 1538 gereicht. Aber da gehe ich mal von Rundungsfehlern bei den weiteren Nachkommastellen aus. Diese kleine Tabelle stellt eines fest: Die Werte sind okay. Das erklärt also nicht die Delle in der Kurvenzeichnung… komisch. Jetzt müsste ich mir die komplette Aufgabe mal aufzeichnen, vom ersten Spiel an, um die ganze Kurve sehen zu können. Gibt es mehrere Knicke? Erkennbare Muster, Auffälligkeiten? Moment, kann Basic-256 nicht auch Grafikausgabe? Könnte ich das nicht genau so coden, wie ich es zeichnerisch ermittelt habe? Klar, das mache ich. Sobald ich Zeit dafür habe. Vermutlich würde ich am Ende feststellen, dass Computer eben doch genauer sind als der Kopfrechnende Mensch.
Falls einer von euch hier lesenden eine Erklärung für den Knick hat: Gerne her damit!
